Verhalten von NS-LS gegenüber Oberwellenströmen - Teil 3

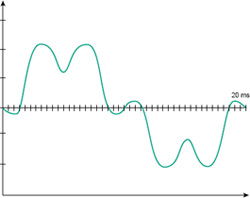
Infolge der Entwicklung der Verbraucher (insbesondere der zunehmenden Verwendung von Stromrichtern) sind die in den Verteilungsnetzen angetroffenen Ströme seit langem keine perfekten 50-Hz-Sinuswellen mehr. In Bezug auf die Messung haben diese Ströme insbesondere im Normalbetrieb bei der Überprüfung der thermischen Auswirkungen einen störenden Einfluss. Bei Fehlerströmen über 10 In ist ihr Einfluss vernachlässigbar.

Theoretische Grundlagen der Oberwellenströme
Nichtlineare und Oberwellen erzeugende Lasten
Das Ohmsche Gesetz drückt die Proportionalität (Linearität) zwischen dem Strom und der Spannung für Sinuswellen bei Netzfrequenz aus. Gewisse (so genannt nichtlineare) Verbraucher deformieren die sinusförmige Stromwelle und folglich auch die Spannungswelle. Dies Deformation kann mit Hilfe einer Fourier-Zerlegung analysiert werden, woraus sich die Oberwellen ergeben, die der Grundwelle überlagert sind und diese deformieren.

Fourier-Zerlegung
Jeder in einem elektrischen Netz auftretende Strom und jede Spannung können durch die Überlagerung einer sinusförmigen Grundwelle mit der Netzfrequenz mit einer Anzahl von sinusförmigen Oberwellen mit Mehrfachen der Netzfrequenz dargestellt werden. Der Ausdruck dieser Größen ist durch die Fourier- Zerlegung der Strom- oder Spannungsfunktion y(t) gegeben:



Yo = Amplitude der Gleichstromkomponente.
Y1 = Effektivwert der sinusförmigen 50-Hz-Komponente (Grundwelle).
ω = Kreisfrequenz der Grundwelle.
φ₁ = Phasenverschiebung der Grundwelle. Yn (für n > 1) = Effektivwert der Oberwelle der n-ten Ordnung.
nω = Kreisfrequenz der n-ten Oberwelle.
φn = Phasenverschiebung der n-ten Oberwelle.

Ohmsches Gesetz
Wenn nichtlineare Verbraucher vorhanden sind, gilt das Ohmsche Gesetz lediglich zwischen dem Strom und der Spannung derselben Ordnung «n» mit einem Impedanzwert für eine Kreisfrequenz, die dem n-fachen der Kreisfrequenz der Grundwelle entspricht:
Un = Z(nω) x In.
Man kann sagen, das für jede Oberwellenordnung die Deformation der Stromwelle eine entsprechende Deformation der Spannungswelle bewirkt, deren Amplitude und Phase vom Wert der Impedanz für jede Oberwellenfrequenz abhängen. Zwischen den Effektivwerten dieser beiden Wellen gibt keine einfache Beziehung mehr.

Effektivwert des deformierten Stroms



was den Stromverzerrungsgrad Di zeigt.

Scheitelfaktor des Stroms



Auswirkungen der Oberwellen

• Auswirkung des Scheitelfaktors:
  • Wenn der Scheitelfaktor größer als √2 ist, besteht die Gefahr einer ungewollten Auslösung, wenn die Schutzeinrichtungen den Ieff aufgrund von IScheitel bestimmen.
  • Wenn der Scheitelfaktor kleiner als √2 ist, besteht die Gefahr einer Überhitzung infolge Nichtauslösung dieser Schutzeinrichtungen.
• Erwärmungen
  dem Nennstrom In bei 50 Hz erhöht sich der Effektivwert des Stroms in den Leitern, weil er mit multipliziert wird, woraus sich folgendes ergibt:
  • Zusätzliche Verluste und somit Überhitzung der Transformatoren, Kabel und Generatoren.
  • Magnetischer Schwund, Erwärmungen und Störmomente in rotierenden Maschinen.
• Fließen von hohen Strömen im Neutralleiter mit Oberwellen der 3. Ordnung und Mehrfachen von 3. Deshalb müssen für den Leiterschutz die thermischen Auslöser den Effektivwert des Stroms in Betracht ziehen.