Berechnung von Kurzschlussströmen - Teil 8

Vorteil dieser Methode
Die Berechnung mit Hilfe symmetrischer Komponenten ist besonders vorteilhaft, wenn ein Drehstromnetz unsymmetrisch ist, weil die sogenannten "zyklischen" klassischen Impedanzen R und X normalerweise nicht mehr verwendbar sind, zum Beispiel infolge von magnetischen Erscheinungen. Ferner ist diese Berechnung in den folgenden Fällen erforderlich:

1. Wenn ein Spannungs- und Stromsystem nicht symmetrisch ist (Fresnelsche Vektoren mit verschiedenen Modulen und von 120° abweichenden Phasenverschiebungen). Dies ist der Fall bei einem einpoligen oder zweipoligen Kurz- oder Erdschluss.
2. Das Netz enthält elektrische Maschinen und/oder Spezialtransformatoren (zum Beispiel der Schaltgruppe Yyn).

Diese Methode ist auf alle Arten von Stromversorgungs-Strahlennetzen unabhängig von der Spannung anwendbar.

Allgemeines über symmetrische Komponenten
So wie das Leblanc-Theorem besagt, dass ein Wechselfeld mit sinusförmiger Amplitude zwei entgegengesetzt umlaufenden Drehfeldern entspricht, beruht die Definition der symmetrischen Komponenten auf der Äquivalenz zwischen einem unsymmetrischen Dreiphasensystem und der Summe von drei symmetrischen Dreiphasensystemen: dem mitlaufenden System, dem gegenlaufenden System und dem Nullsystem (siehe Abb. 21).



Das Überlagerungsprinzip ist nun auf die Berechnung von Kurzschlussströmen anwendbar. Für die nachfolgende Erklärung wird das System dadurch definiert, dass man den Strom als Drehreferenz nimmt, und

• als seine mitlaufende Komponente,
• als seine gegenlaufende Komponente,
• als seine Nullkomponente, und indem man den Operator verwendet.

Die Anwendung dieses Prinzips auf ein System von Strömen lässt sich durch grafische Konstruktion überprüfen (siehe Abb. 21). So ergibt zum Beispiel die grafische Addition der Vektoren für :



Die Ströme werden auf dieselbe Weise ausgedrückt, woraus sich das folgende System ergibt:



Diese symmetrischen Stromkomponenten sind über die entsprechenden Impedanzkomponenten mit den symmetrischen Spannungskomponenten verbunden:



Diese Impedanzen können aufgrund der (von den Herstellern angegebenen) Eigenschaften der einzelnen Betriebsmittel des untersuchten Stromnetzes definiert werden. Zu diesen Eigenschaften ist zu bemerken, dass Zi ≈ Zd (außer für elektrische Maschinen), während Zo je nach Betriebsmittel variiert (siehe Abb. 22).

Berechnung nach IEC 909
Die Norm IEC 909 enthält ein Verfahren, das von nicht spezialisierten Ingenieuren angewendet werden kann und die symmetrischen Komponenten verwendet. Dieses Verfahren ist für Stromnetze mit einer Spannung unterhalb von 230 kV anwendbar. Es beschreibt die Berechnung der maximalen und minimalen Kurzschlussströme. Die ersteren dienen dazu, die Bemessungsdaten der Betriebsmittel zu bestimmen. Die letzteren werden für die Kalibrierung der Überstromschutzeinrichtungen benötigt. Diese Norm wird für ihre Anwendung auf NS-Netze durch den Leitfaden IEC 781 ergänzt.

Verfahren

1. Berechnung der Ersatzspannung an der Fehlerstelle gleich
   
   
   
   anbei ist c ein Spannungsfaktor, der in die Berechnungen eingeführt werden muss, um: die örtlichen und zeitlichen Spannungsschwankungen, eventuelle Änderungen der Stufenschalter der Transformatoren, das subtransiente Verhalten der Generatoren und Motoren zu berücksichtigen. In der Abbildung 23 sind die normativen Werte dieses Spannungsfaktors in Funktion der durchzuführenden Berechnungen und der betrachteten Spannungsebenen angegeben.
   
   
   
   
2. Bestimmung und Addition der direkten, inversen und Null-Ersatzimpedanzen auf der Speisungsseite der Fehlerstelle.
   
   
3. Berechnung des Anfangskurzschlussstroms mit Hilfe symmetrischer Komponenten. Die in der Praxis je nach Art des Kurzschlusses für die Berechnung der Icc anzuwendenden Formeln sind in der Tabelle der Abbildung 24 enthalten.
   
   Klicken Sie auf das Bild für eine größere Ansicht
   
   
4. Aufgrund des Wertes von Icc (Ik“), Berechnung der übrigen Größen, wie zum Beispiel des Spitzenwertes von Icc, des stationären Wertes von Icc oder auch des maximalen stationären Wertes von Icc.

Einfluss der Distanz zwischen der Fehlerstelle und dem Generator
Bei dieser Berechnungsmethode müssen immer zwei Fälle unterschieden werden:

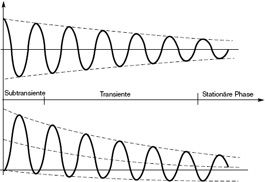
• Fall der generatorfernen Kurzschlüsse, der den Netzen entspricht, in denen die Kurzschlussströme keine abklingende Wechselstromkomponente haben. Dies ist im Allgemeinen in der NS der Fall, außer wenn Verbraucher mit hoher Stromaufnahme über spezielle Transformatorstationen gespeist werden.
  
  
• Fall der generatornahen Kurzschlüsse (siehe Abb. 11), der den Netzen entspricht, in denen die Kurzschlussströme abklingende Wechselstromkomponenten haben. Dieser Fall tritt im Allgemeinen in der Hochspannung auf. Er kann jedoch in der Niederspannung vorkommen, wenn zum Beispiel ein Notstrommaggregat mit Priorität versehene Abgänge speist.
  
  

Die wesentlichen Unterschiede zwischen diesen beiden Fällen sind:

• Bei den generatorfernen Kurzschlüssen besteht Übereinstimmung zwischen dem Anfangskurzschlussstrom (Ik"), dem Dauerkurzschlussstrom (Ik) und dem abgeschalteten Kurzschlussstrom (Ib) einerseits (Ik" = Ik = Ib);
  
  
• und zwischen der direkten (Zd) und der inversen (Zi) Impedanz andererseits (Zd = Zi).

Bei den generatornahen Kurzschlüssen wird hingegen die folgende Ungleichung überprüft: Ik < Ib < Ik“, und zudem Zd, welche Impedanz nicht unbedingt gleich Zi ist. Dazu ist jedoch zu bemerken, dass auch Asynchronmotoren eine Kurzschluss speisen können, wobei deren Beitrag innerhalb der ersten 30 Millisekunden 30% des Icc des Netzes erreichen kann. In diesem Fall stimmt die Gleichung Ik“ = Ik = Ib nicht mehr.

Für die Berechnung der minimalen und maximalem Kurzschlussströme einzuhaltende Bedingungen
Die Berechnung der maximalen Kurzschlussströme berücksichtigt die folgenden Punkte:

• Den anzuwendenden Spannungsfaktor c, welcher der Berechnung des maximalen Kurzschlussstromes entspricht.
• Sämtliche in diesem Dokument aufgeführten Annahmen und Näherungen, wobei nur jene in Betracht gezogen werden dürfen, die zu Werten führen, die auf der sicheren Seite liegen.
• Die Widerstände R_L der Leitungen (Freileitungen, Kabel, Phasen- und Neutralleiter) für eine Temperatur von 20 °C.

Für die Berechnung der minimalen Kurzschlussströme

• muss der Spannungsfaktor c angewendet werden, welcher der im Netz zulässigen Mindestspannung entspricht,
• muss die Netzkonfiguration gewählt werden, und in bestimmten Fällen die minimale Speisung durch Quellen und Leitungen, die an der Fehlerstelle den Minimalwert des Kurzschlussstromes bewirken,
• muss die Impedanz der Sammelschienen, der Stromwandler usw. berücksichtigt werden,
• müssen die Motoren unbeachtet bleiben,
• muss der Widerstand R_L für die höchste zu erwartende Temperatur gewählt werden:
  
  
  
  wobei R_L20 der Widerstand bei der Temperatur 20 °C und θe die für den Leiter am Ende des Kurzschlusses zulässige Temperatur (in °C) ist. Der Faktor 0,004/°C gilt für Kupfer, Aluminium und die Aluminiumlegierungen.