Berechnung von Kurzschlussströmen - Teil 3

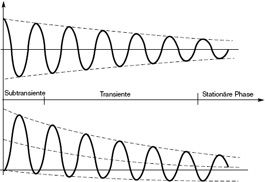
Icc in Abhängigkeit von der Kurzschlussart
Dreipoliger Kurzschluss
Dieser Fehler entspricht der Zusammenschaltung der drei Phasen. Der Kurzschlussstrom Icc3 beträgt:



wobei U (verkettete Spannung) der Leerlaufspannung des Transformators entspricht, die um 3 bis 5% höher liegt als die Klemmenspannung unter Last. In einem 390-V-Netz zum Beispiel beträgt die angenommene Spannung U = 410 V mit einer Phasenspannung von .

Die Berechnung des Kurzschlussstroms reduziert sich somit auf die Berechnung der Impedanz Zcc, der Ersatzimpedanz aller von Icc durchflossenen Impedanzen (der Quelle und der Leitungen) vom Generator bis zur Fehlerstelle (siehe Abb. 12). Dies ist effektiv die "direkte" Impedanz pro Phase:



∑R = Summe der in Serie geschalteten Widerstande
∑X = Summe der in Serie geschalteten Reaktanzen

Der dreipolige Fehler gilt als jener, der die höchsten Fehlerströme erzeugt. Effektiv wird der Fehlerstrom im Ersatzschema eines Mehrphasensystems nur durch die Impedanz einer Phase unter der Phasenspannung des Netzes begrenzt. Somit ist die Berechnung von Icc3 unerlässlich, um die Betriebsmittel (in Bezug auf die auszuhaltenden Stromstärken und elektrodynamischen Beanspruchungen) auswählen zu können.

Isolierter zweipoliger Kurzschluss
Dieser entspricht einem von der verketteten Spannung U gespeisten Fehler zwischen zwei Phasen. Der dabei auftretende Strom Icc2 ist kleiner als bei einem dreipoligen Fehler:



Isolierter einpoliger Kurzschluss
Dieser entspricht einem von der Phasenspannung gespeisten Fehler zwischen einer Phase und dem Neutralleiter. Der dabei auftretende Strom Icc1 beträgt:



In bestimmten Fällen eines einpoligen Fehlers ist die Nullimpedanz der Quelle niedriger als Zcc (zum Beispiel an den Klemmen eines Transformators in Stern-Zickzack-Schaltung oder eines Generators im subtransienten Zustand. Der Strom kann dann bei einem einpoligen Fehler höher sein als bei einem dreipoligen Fehler.

(Einpoliger oder zweipoliger) Erdschluss
Bei einem solchen Fehler kommt die Nullimpedanz Zo zur Wirkung. Außer beim Vorhandensein von elektrischen Maschinen, bei denen die Nullimpedanz reduziert ist, ist der auftretende Strom Icch niedriger als beim dreipoligen Kurzschluss. Seine Berechnung kann je nach der Sternpunktbehandlung (dem Erdungsschema) für die Wahl der Einstellwerte der gleichpoligen (HS) oder differentiellen (NS) Schutzeinrichtungen erforderlich sein.

Zusammenfassende Tabelle der verschiedenen Kurzschlussströme
(siehe Abb. 12).


 

Bestimmung der verschiedenen Kurzschlussimpedanzen
Das Prinzip dieser Methode besteht darin, die Kurzschlussströme aufgrund der Impedanz des vom Kurzschlussstrom durchflossenen "Stromkreises" zu bestimmen. Diese Impedanz wird berechnet, nachdem man separat die einzelnen Widerstände und Reaktanzen der Fehlerschleife von einschließlich der Stromversorgungsquelle bis zur betrachteten Stelle addiert hat. (Die Nummern (X) dienen dazu, im Beispiel am Schluss dieses Kapitels die im Text enthaltenen Erklärungen leicht zu finden.)

Impedanzen des Netzes

Impedanz des vorgeschalteten Netzes
In den meisten Berechnungen geht man speisungsseitig nicht weiter als bis zur Übergabestelle der Energie. Die Kenntnis des vorgeschalteten Netzes beschränkt sich somit in der Regel auf die vom Versorgungsunternehmen gelieferten Angaben, d.h. lediglich die Kurzschlussleistung Scc (in MVA). Die Ersatzimpedanz des vorgeschalteten Netzes beträgt:
(1) ⇒
U ist die verkettete Spannung des unbelasteten Netzes.
Der vorgeschaltete Widerstand und die vorgeschaltete Reaktanz können aufgrund von Ra/Za in der HS ermittelt werden:
Ra / Za . 0,3 in 6 kV,
Ra / Za . 0,2 in 20 kV,
Ra / Za . 0,1 in 150 kV.

(2) ⇒ Xa = 0,980 Za in 20 kV,

Innere Impedanz des Transformators
Die Impedanz berechnet sich aus der Kurzschlussspannung ucc ausgedrückt in %:
(3) ⇒

U = Verkettete Leerlaufspannung des Transformators
Sn = Scheinleistung des Transformators
U . ucc = Spannung, die auf der Primärseite des Transformators angelegt werden muss, damit die Sekundärseite bei kurzgeschlossenen sekundärseitigen NS-Klemmen vom Nennstrom In durchflossen wird.

Für HS/NS-Speisetransformatoren der öffentlichen Stromversorgung sind die Werte von ucc von der EDF (HN52 S20) und in einem europäischen Normenentwurf (PR-HD 428.1S1) festgelegt (siehe Abb. 13). In diesem Zusammenhang ist zu bemerken, dass die Genauigkeit dieser Werte einen unmittelbaren Einfluss auf die Berechnung der Icc hat, weil ein Fehler von x% für ucc einen Fehler von der gleichen Größenordnung (x%) für ZT bewirkt.



(4) ⇒ Normalerweise RT << XT, in der Größenordnung von 0,2 XT, wobei die innere Impedanz der Transformatoren mit der Reaktanz XT gleichgesetzt werden kann. Für kleine Leistungen ist hingegen die Berechnung von ZT notwendig, da das Verhältnis RT/XT größer ist. Dieser Widerstand wird somit wie folgt aus den ohmschen Verlusten (W) in den Wicklungen berechnet:



Anmerkungen:
(5) ⇒ Wenn n Transformatoren von gleicher Leistung parallel geschaltet sind, müssen ihre Werte für die innere Impedanz sowie den Widerstand oder die Reaktanz durch n dividiert werden.
Besondere Beachtung muss den Spezialtransformatoren geschenkt werden. Zum Beispiel die Transformatoren der Gleichrichtergruppen haben Werte von ucc, die 10 bis 12% erreichen, um den Kurzschlussstrom zu begrenzen. Unter Berücksichtigung der Impedanz auf der Speisungsseite des Transformators und der inneren Impedanz des Transformators kann der Kurzschlussstrom wie folgt ausgedrückt werden:



In erster Näherung können Za und ZT mit ihren Reaktanzen gleichgesetzt werden. Die Kurzschlussimpedanz Zcc ist dann gleich ihrer algebraischen Summe.

Die Impedanz des vorgeschalteten Netzes kann in diesem Fall vernachlässigt werden, wobei der neue Wert des Kurzschlussstroms beträgt:



Die Abbildung 14 zeigt den zusätzlichen Fehler bei der Berechnung von Icc, wenn die vorgschaltete Impedanz vernachlässigt wird. Diese Abbildung zeigt sehr gut, dass die vorgeschaltete Impedanz bei Netzen vernachlässigt werden kann, deren Kurzschlussleistung Scc im Verhältnis zur Leistung Sn des Transformators hoch ist. So beträgt für Scc/ Sn = 300 der Fehler etwa 5%.