Berechnung von Kurzschlussströmen - Teil 2

Fehler in großer Entfernung von den Generatoren
Dies ist der häufigste Fall. Der Ausgleichsvorgang ist dabei derjenige, der bei der Anwendung eines aus einer Induktivität und einem Widerstand bestehenden Stromkreises mit der Spannung
e = E . sin (ω . t + α)
entsteht.

Der Strom i ist dabei die Summe der beiden Komponenten i = ia + ic.

Die eine Komponente (ia) ist die sinusförmige Wechselstromkomponente
ia = I . sin (ω . t + α) wobei
I = Maximalwert des Stroms = E/Zcc,
α = elektrischer Winkel zwischen dem Auftreten des Fehlers und dem Nulldurchgang der Spannungswelle

Die andere Komponente (ic) ist die Gleichstromkomponente . Ihr Anfangswert hangt von ƒ¿ ab und ihr Abklingen ist umso schneller, je größer R/L ist.
Zu Beginn des Kurzschlusses ist i definitionsgemäß gleich null (wenn man den Betriebsstrom Is vernachlässigt), woraus:
i = ia + ic = 0

Die Abbildung 7 zeigt den grafischen Aufbau von i durch algebraische Addition der Ordinaten der beiden Komponenten ia und ic.



Die Abbildung 8 zeigt die beiden möglichen Extremfälle für die Entstehung eines Icc, die zum einfacheren Verständnis durch eine Einphasen-Wechselspannung dargestellt werden.



Der Faktor ist umso höher, je kleiner das Verhältnis R/L bzw. R/X und damit je schwächer das Abklingen der Gleichstromkomponente ist. Somit muss ip berechnet werden, um das Ausschaltvermögen der zu liefrenden Leistungsschalter zu bestimmen, jedoch auch, um die elektrodynamischen Belastungen zu ermitteln, welche die gesamte Anlage auszuhalten in der Lage sein muss. Dieser Wert kann aufgrund der folgenden Beziehung aus dem Effektivwert des symmetrischen Kurzschlussstroms abgeleitet werden:
wobei der Koeffizient K der Kurve der Abbildung 9 in Funktion des Verhältnisses R/X bzw. R/L entnommen werden kann.
 

Fehler in der Nähe der Generatoren
Wenn der Fehler in der unmittelbaren Nähe des den betreffenden Stromkreis speisenden Generators auftritt, bewirkt die nunmehr vorherrschende Änderung der Impedanz des Generators eine Abschwächung des Kurzschlussstroms. Effektiv wird der Ausgleichsvorgang, aus dem der Kurzschlussstrom entsteht, durch die sich aus dem Kurzschluss ergebende Änderung der EMK (elektromotorischen Kraft) kompliziert. Zur Vereinfachung nimmt man die EMK als konstant an, jedoch die innere Reaktanz der Maschine als variabel. Diese Reaktanz ändert sich je nach den drei Phasen:
 

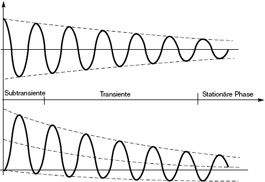
1. Subtransiente Reaktanz, die während der ersten 10 bis 20 Millisekunden des Fehlers auftritt.
2. Transiente Reaktanz, die bis zu 500 Millisekunden dauern kann.
3. Stationäre Reaktanz oder synchrone Reaktanz.

Dazu ist zu bemerken, dass die Reaktanz in jeder Phase in der angegebenen Reihenfolge zunimmt: die subtransiente Reaktanz ist kleiner als die transiente Reaktanz, und diese wiederum kleiner als die stationäre Reaktanz. Diese Zunahme der Reaktanz bewirkt eine Abnahme des Kurzschlussstroms, der somit die Summe von vier Komponenten ist (siehe Abb. 10):

1. Den drei Wechselstromkomponenten (subtransiente, transiente und stationäre Komponente).
2. Der Gleichstromkomponente als Ergebnis der Entstehung des Stroms im (induktiven) Stromkreis.

In der Praxis ist die Kenntnis des Verlaufes des Kurzschlussstroms nicht immer unerlässlich:

In der Niederspannung genügt wegen der Schnelligkeit der Abschalteinrichtungen die Kenntnis des mit I"k bezeichneten subtransienten Kurzschlussstroms sowie des maximalen unsymmetrischen Scheitelwertes ip für die Bestimmung des ASV der Schutzeinrichtungen und der elektrodynamischen Beanspruchungen.

In der Niederspannungsverteilung und in der Hochspannung wird hingegen der transiente Kurzschlussstrom oft verwendet, wenn die Abschaltung erfolgt, bevor der Dauerkurzschlussstrom erreicht ist. Es ist deshalb von Vorteil, den abgeschalteten Kurzschlussstrom In einzuführen, der das ASV der verzögerten Leistungsschalter bestimmt. Ib ist der Wert des Kurzschlussstroms im Moment der effektiven Unterbrechung und somit nach der Zeit t nach dem Auftreten des Kurzschlusses, wobei t = tmin. Die Zeit tmin (minimale Totzeit) ist die Summe der minimalen Verzögerung (Verzögerungszeit) eines Schutzrelais und der kürzesten Öffnungszeit des damit verbundenen Leistungsschalters. Es handelt sich um die kürzeste Zeit, die zwischen dem Auftreten des Kurzschlussstroms und der ersten Trennung der Kontakte eines Poles des Schaltgerätes verstreicht.

Die Abbildung 11 zeigt die so definierten Kurzschlussströme.


 

Normen und Berechnungen der Icc
Von den Normen werden verschiedene Methoden vorgeschlagen. Der Anwendungs-Leitfaden UTE C 15-105, nach franz. Norm, enthält die folgenden vier Methoden:

1. Die "Impedanzen"-Methode, mit der die Fehlerströme an jeder Stelle der Anlage mit ziemlicher Genauigkeit berechnet werde können. Sie besteht darin, die einzelnen Widerstände und Reaktanzen der Fehlerschleife von einschließlich der Quelle bis zur betrachteten Stelle zu addieren und hierauf die entsprechende Impedanz zu berechnen. Schließlich wird der Icc mit Hilfe des Ohmschen Gesetzes erhalten: Icc = Un / ∑(Z). Alle Eigenschaften der einzelnen Teile der Fehlerschleife (Quellen und Leitungen) müssen bekannt sein.
    
2. Die "Zusammensetzungs"-Methode, die angewendet werden kann, wenn die Eigenschaften der Speisung nicht bekannt sind. Die speisungsseitige Impedanz des betrachteten Stromkreises wird aufgrund des Kurzschlussstroms an der Einspeisung berechnet. Der Leistungsfaktor cos φcc = R/X wird als an der Einspeisung und an der Fehlerstelle identisch angenommen. Mit anderen Worten entspricht dies der Annahme, dass die Elementarimpedanzen der beiden aufeinander folgenden Abschnitte der Anlage genügend benachbarte Argumente haben, um die vektorielle Addition durch eine algebraische Addition der Impedanzen zu ersetzen. Aufgrund dieser Näherung kann man den Wert des Moduls der Kurzschlussströme mit genügender Genauigkeit erhalten, um einen Stromkreis hinzuzufügen. Diese angenäherte Methode kann nur für Anlagen mit einer Leistung unter 800 kVA angewendet werden.
    
3. Die sogenannte "konventionelle" Methode, welche die Möglichkeit bietet, die minimalen Kurzschlussströme und die Fehlerströme am Ende einer Leitung zu berechnen, ohne die Impedanzen oder die Icc des dem betreffenden Stromkreis vorgeschalteten Teils der Anlage zu kennen. Sie beruht auf der Annahme, dass die Spannung an der Einspeisung während der Dauer des Kurzschlusses bzw. des Fehlers gleich 80% der Nennspannung der Anlage ist. Sie berücksichtigt nur den Widerstand der Leiter, auf den sie, um auch ihre Induktivität zu berücksichtigen, für große Querschnitte einen Erhöhungsfaktor (1,15 für 150 mm², 1,20 für 185 mm² usw.) anwendet. Diese Methode gelangt vor allem für Verbraucherstromkreise zur Anwendung, deren Einspeisepunkt genügend weit entfernt von der Speisequelle ist (Gruppennetz).
    
4. Die sogenannte "vereinfachte" Methode (im gleichen Leitfaden im Detail dargestellt), die mit Hilfe von aufgrund von zahlreichen vereinfachenden Annahmen erstellten Tabellen für jeden Leiterquerschnitt direkt die folgenden Angaben liefert:
   • Bemessungsstrom der Einrichtung, die den Überlastschutz sicherstellt,
   • maximale Länge der gegen indirektes Berühren geschützten Leitungen,
   • vom Gesichtspunkt der Spannungsabfälle zulässige Längen.
   Diese Tabellen enthalten effektiv die Resultate von im Wesentlichen mit der Zusammensetzungs- und der konventionellen Methode durchgeführten Berechnungen. Diese Methode bietet die Möglichkeit, die Eigenschaften eines Stromkreises zu bestimmen, der einer bestehenden Anlage hinzugefügt wird, dessen Eigenschaften nicht genügend bekannt sind. Sie ist direkt auf Niederspannungsanlagen anwendbar, und zwar mit Korrekturfaktoren, wenn die Spannung verschieden von 230/400 V ist.

Die Methode nach der Norm IEC 909 (VDE 0102) ist für alle Strahlen- und Maschennetze bis 230 kV anwendbar. Sie besteht darin, eine Ersatz-Spannungsquelle an der Kurzschlussstelle zu berechnen, um hierauf den Strom an dieser Stelle zu bestimmen. Alle Einspeisungen des Netzes sowie Synchron- und Asynchronmaschinen werden durch ihre Impedanzen (direkte, indirekte und Nullimpedanz) ersetzt. Bei dieser Methode werden alle Leitungskapazitäten und Paralleladmittanzen der nicht rotierenden Lasten außer jenen des Nullsystems vernachlässigt.

Es gibt noch weitere Methoden. Sie beruhen auf dem Überlagerungsprinzip und erfordern eine vorherige Berechnung des Laststroms. Ferner muss auf die Methode der Norm IEC 865 (VDE 0103) hingewiesen werden, die zur Berechnung des thermisch äquivalenten Kurzschlussstroms führt.

Die in diesem Technischen Heft behandelten Methoden
In diesem Technischen Heft werden speziell zwei Methoden für die Berechnung der Kurzschlussströme in Strahlennetzen behandelt:

1. Bei der einen Methode, die vor allem für Niederspannungsnetze angewendet wird, handelt es sich um die Impedanzenmethode. Sie wurde wegen der mit ihr möglichen Genauigkeit gewählt, sowie angesichts ihres didaktischen Wertes, da dabei praktisch alle Eigenschaften des betreffenden Stromkreises in Betracht gezogen werden müssen.
    
2. Die andere Methode, die vorwiegend in der Hochspannung Anwendung findet, ist jene nach IEC 909, die wegen ihrer Genauigkeit und ihres analytischen Gesichtspunktes ausgewählt wurde. Technisch wendet sie das Prinzip das symmetrischen Komponenten an.

Grundlegende Annahmen
Für diese Kurzschlussstromberechnungen müssen Annahmen getroffen werden, die den Gültigkeitsbereich der gegebenen Formeln festlegen. Diese oft vereinfachenden und mit begründeten Näherungen verbundenen Annahmen erleichtern das Verständnis der physikalischen Vorgänge und damit der Berechnungen unter gleichzeitiger Aufrechterhaltung einer in jeder Beziehung genügenden Genauigkeit. Die in diesem Dokument gewählten Annahmen sind:

• Das betrachtete Netz ist ein Strahlennetz, und seine Nennspannung reicht von der Niederspannung bis zur Hochspannung (übersteigt jedoch den in der Norm IEC 909 angegeben Wert von 230 kV nicht).
• Bei einem dreipoligen Kurzschluss tritt der Kurzschlussstrom an allen drei Phasen gleichzeitig auf.
• Während der Dauer des Kurzschlusses ändert sich die Anzahl der betroffenen Phasen nicht. Ein dreipoliger Kurzschluss bleibt dreipolig, und ein einpoliger Erdschluss bleibt ein einpoliger Erdschluss.
• Während der gesamten Kurzschlussdauer ändern sich die Spannungen, die das Fliessen des Stroms bewirkt haben, sowie die Kurzschlussimpedanz nicht wesentlich.
• Die Regler oder Stufenschalter der Transformatoren befinden sich in ihrer mittleren Stellung (bei einem generatorfernen Kurzschluss können die wirklichen Stellungen dieser Stufenschalter außer acht gelassen werden).
• Die Lichtbogenwiderstände werden nicht berücksichtigt.
• Sämtliche Leitungskapazitäten werden vernachlässigt.
• Die Lastströme werden vernachlässigt.
• Alle Nullimpedanzen werden berücksichtigt.