Berechnung der Icc mit der Impedanzenmethode - Leitungsimpedanz und Impedanz elektrischer Maschinen
Die Leitungsimpedanz ZL hängt vom Widerstands- und Reaktanzbelag und von der Länge der Leitungen ab. Der Widerstandsbelag RL von Freileitungen, Kabeln und Sammelschienen berechnet sich mit der Formel:
wobei:
S = Leiterquerschnitt
p = Spezifischer Widerstand des Leiters, wobei jedoch der anzuwendende Wert je nach dem berechneten maximalen oder minimalen Kurzschlussstrom verschieden ist.
(6) ⇒ Die Tabelle der Abbildung 15 enthält diese Werte für jeden einzelnen Fall.

In Wirklichkeit wird in der Niederspannung und für Leiterquerschnitte unter 150 mm² nur der Widerstand berücksichtigt (für S > 150 mm² ist RL < 0,15 mΩ/m).
Der Reaktanzbelag XL von Freileitungen, Kabeln und Sammelschienen berechnet sich mit der Formel
ausgedruckt in mΩ/km für ein im Dreieck angeordnetes ein- oder dreipoliges Kabelsystem mit
r = Radius der Leiteradern
d = mittlerer Abstand zwischen den Leitern.
NB: Log = Logarithmus zur Basis 10.
mit dem Abstand der Leiter (proportional zu
(7) ⇒ Die folgenden Mittelwerte muss man sich merken:
X = 0,3 Ω/km (NS- oder MS-Leitungen)
X = 0,4 Ω/km (MS- oder HS-Leitungen)
Für Kabel fasst die Abbildung 16 verschiedene Reaktanzwerte für die Niederspannung in Funktion der Verlegungsart zusammen.

Die folgenden Mittelwerte muss man sich merken:
0,08 mΩ/m für ein Dreileiterkabel
(8) ⇒ 0,09 mΩ/m für (in einer Ebene
(9) ⇒ und 0,15 mΩ/m als Standard für Sammelschienen
Für SS mit mehrlagige angeordneten Phasen (Canalis-Typ von Telemecanique) ist diese Reaktanz wesentlich niedriger.
Anmerkungen:
Die Impedanz kurzer Verbindungen zwischen dem Verteilpunkt und dem HS/NS-Transformator kann vernachlässigt werden, wenn man einen zusätzlichen Fehler in Bezug auf den Kurzschlussstrom in Kauf nimmt. Dieser Fehler ist umso größer, je höher die Transformatorleistung ist.
Die Kapazität der Kabel gegen Erde (äußerer Modus) ist 10- bis 20-mal so groß wie jene der Freileitungen und muss für Erdfehler berücksichtigt werden. Als Richtwert betragt die Kapazität eines Drehstrom-Hochspannungskabels mit einem Leiterquerschnitt von 120 mm² ungefähr 1 µ/km. Der kapazitive Strom bleibt jedoch mit etwa 5 A/km bei 20 kV niedrig.
Der Widerstand oder die Reaktanz der Leitungen kann vernachlässigt werden. Wenn eine der Größen RL oder XL gegenüber der anderen klein ist, kann sie vernachlässigt werden, da in diesem Fall der Fehler in Bezug auf die Impedanz ZL klein ist. Beispielsweise bei einem Verhältnis von 3 zwischen RL und XL beträgt der Fehler in Bezug auf ZL 5,1%.
Aufgrund der Kurven von RL und XL wie jenen der Abbildung 17 können die Kabelquerschnitte bestimmt werden, für welche die Impedanz dem Widerstand oder der Reaktanz gleichgesetzt werden kann.
Beispiel - 1. Fall:
Drehstromkabel bei 20 °C, dessen Leiter aus Kupfer bestehen. Deren Reaktanz beträgt 0,08 mΩ/m. Die Kurven von RL und XL (siehe Abb. 17) zeigen, dass die Impedanz ZL zwei Asymptoten hat, die Gerade RL bei den kleinen Querschnitten und die Gerade XL = 0,08 mΩ/m bei den großen Querschnitten. Für diese Querschnitte ist es somit möglich, anzunehmen, dass die Kurve der Impedanz ZL in die Asymptoten übergeht.
Die Impedanz des betrachteten Kabels ist somit mit einem Fehler von weniger als 5,1%
- für Querschnitte unter 74 mm² ein ohmscher Widerstand,
- für Querschnitte über 660 mm² eine Reaktanz.
Drehstromkabel bei 20 °C, dessen Leiter aus Aluminium bestehen.
Wie im obigen Fall geht die Kurve der Impedanz ZL in ihre Asymptoten über, jedoch für Querschnitte unter 120 mm² bzw. über 1000 mm² (die Kurven sind hier nicht dargestellt).
Die Impedanzen elektrischer Maschinen werden in der Regel in Prozenten ausgedrückt:
Icc / In = 100/e (wobei e das Pendant zum ucc der Transformatoren ist). Somit:
(10) ⇒
U = Verkettete Leerlaufspannung des Generators
Sn = Scheinleistung (VA) des Generators
(11) ⇒ Zudem geht, da R/X klein ist und in der Hochspannung 0,05 bis 0,1 und in der Niederspannung 0,1 bis 0,2 beträgt, die Impedanz Z in die Reaktanz X über. Werte für e sind in der Tabelle der Abbildung 18 für Turbogeneratoren und (mit niedrigeren Drehzahlen laufende) "Wasserkraftwerks"– Schenkelpolgeneratoren angegeben.
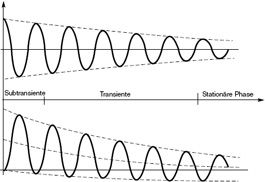
Beim naheren Betrachten dieser Tabelle kann es erstaunen, dass die stationären Kurzschlussreaktanzen 100% übersteigen können (in diesem Moment ist Icc < In). Der Kurzschlussstrom ist jedoch im Wesentlichen induktiv und braucht die gesamte Blindenergie, welche die selbst übererregte Erregerwicklung liefern kann, wahrend der Nennstrom die von der Turbine gelieferte Wirkleistung überträgt (cos φ von 0,8 bis 1). Impedanz elektrischer Maschinen - Synchronmotoren und -phasenschieber.
Das Kurzschlussverhalten dieser Maschinen ist demjenigen der Generatoren ähnlich.
(12) ⇒ Sie geben einen Strom in das Netz ab, der von ihrer Reaktanz in % anhängt (siehe Abbildung 19). Impedanz elektrischer Maschinen - Asynchronmotoren.
Ein plötzlich vom Netz abgetrennter Asynchronmotor hält an seinen Klemmen eine Spannung aufrecht, die in wenigen Hundertstelsekunden abklingt. Wenn an diesen Klemmen ein Kurzschluss auftritt, liefert demnach der Motor einen Strom, der noch schneller abklingt, mit einer Zeitkonstante von ungefähr:
- 2/100 s für Motoren mit Einfachkäfigläufer bis 100 kW,
- 3/100 s für Motoren mit Doppelkäfigläufer und Motoren über 100 kW,
- 3 bis 10/100 s für sehr große Hochspannungsmotoren (1000 kW) mit Schleifringläufer.
Auch ist die große Anzahl der Niederspannungsmotoren niedriger Einheitsleistung in den Industrieanlagen eine Überlegung wert, da es schwierig ist, die durchschnittliche Zahl der in Betrieb stehenden Motoren vorauszusehen, die den Fehler im Moment eines Kurzschlusses speisen. Somit ist es aufwendig und nutzlos, den Rückstrom jedes Motors unter Berücksichtigung seiner Rückwirkungsimpedanz zu berechnen. Deshalb ist es (insbesondere in den USA) üblich, den Beitrag aller Niederspannungs- Asynchronmotoren einer Anlage zum Fehlerstrom global zu betrachten.
(13) ⇒ Sie werden somit mit einer einzigen Quelle verglichen, die einen Strom an die Sammelschienen liefert, der gleich dem 3fachen der Summe der Nennströme aller installierten Motoren ist.